SS-V:9002 充填された導波管内の波の伝播
テスト番号VE03充填された導波管内における、基本モード波の伝搬
定義
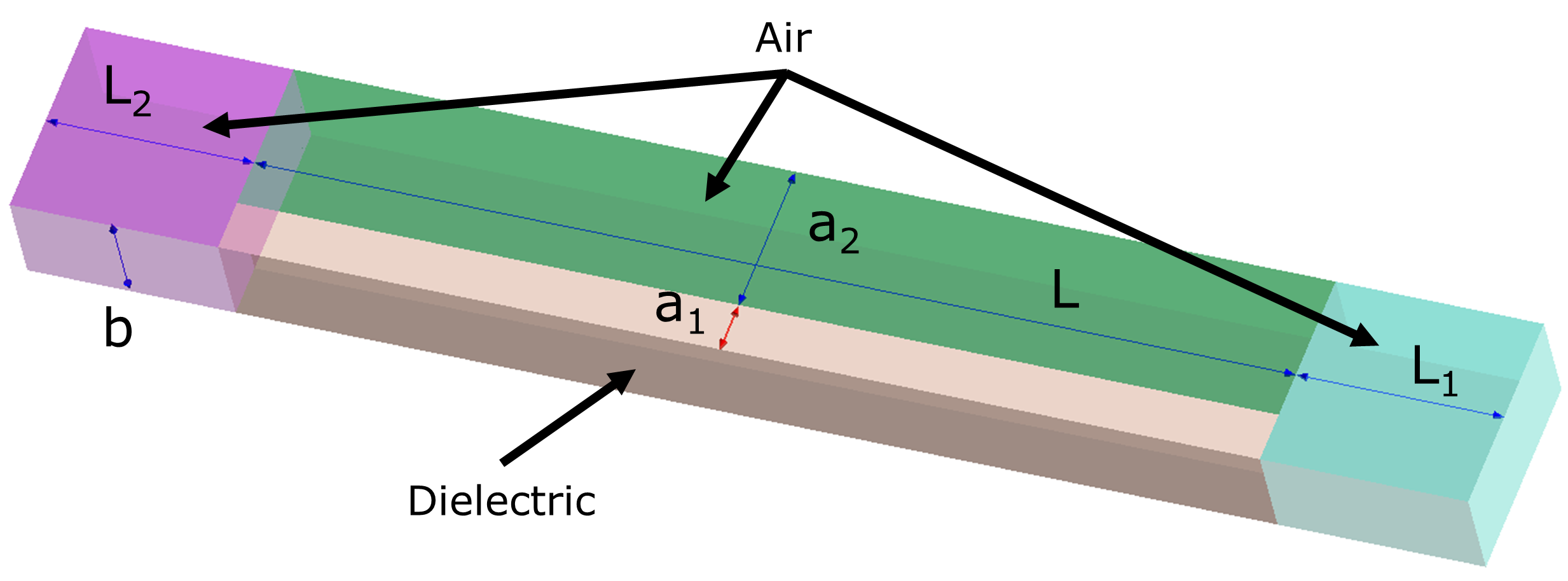
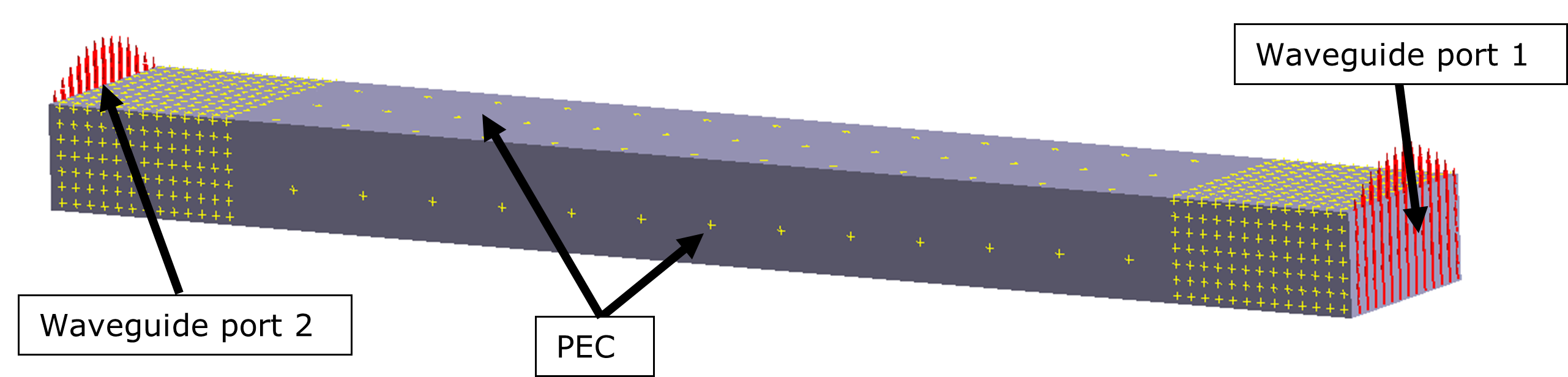
- Figure 1:a1 = 5mm、a2 = 15mm、a = a1 + a2、b = 10 mm、L = 100 mm、L1 = L2 = 20 mm
- すべての側壁はPEC(完全電気導体)条件とし、端面は導波管ポートとなります
- 特性
- 値
- 誘電体の比誘電率( )
- 4.0
- 誘電体の比透磁率( )
- 1.0
- 空気の比透磁率( )
- 1.0
- 空気の比透磁率( )
- 1.0
基準解
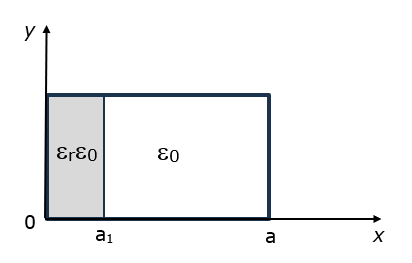
縦磁場の方程式は次のようになります。
モデルパラメータの組み合わせによって、 と の両方が正、または が正で は負になります。
最初のケースの の値は次の方程式の解から得られます。
これは、1の定義に基づいて、 と を代入したものです。
が負の値の場合、同様の方法で、 の値が方程式の解から得られます(このケースは、Pozarの1のケースを補完)。
1つ目のケースの電場の分布は以下のようになります。Figure 4.
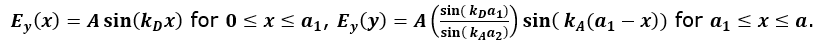
Figure 5.
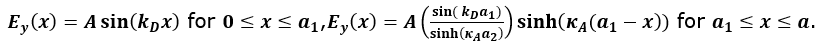
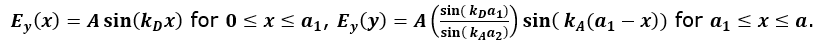
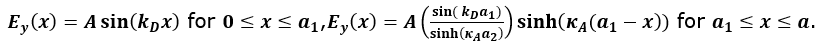
結果
の場合には方程式(1)が有効であり、
では方程式(2)を使用する必要があります。Figure 6. 導波管ポート1がアクティブで、f = 7.5Ghzにおける電界
の分布

Figure 7. 上の図のラインに沿った理論上およびモデル化された電界分布の比較
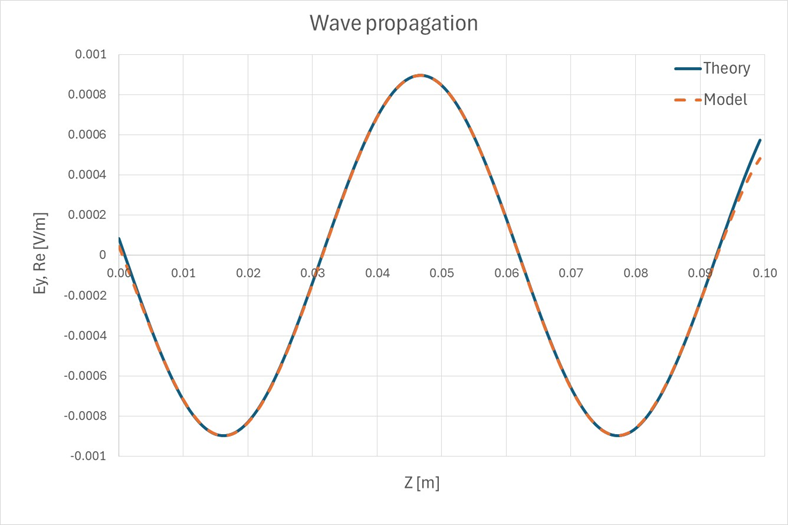
Figure 8. 導波管ポート1がアクティブで、f = 10Ghzにおける電界
の分布

Figure 9. 上の図のラインに沿った理論上およびモデル化された電界分布の比較
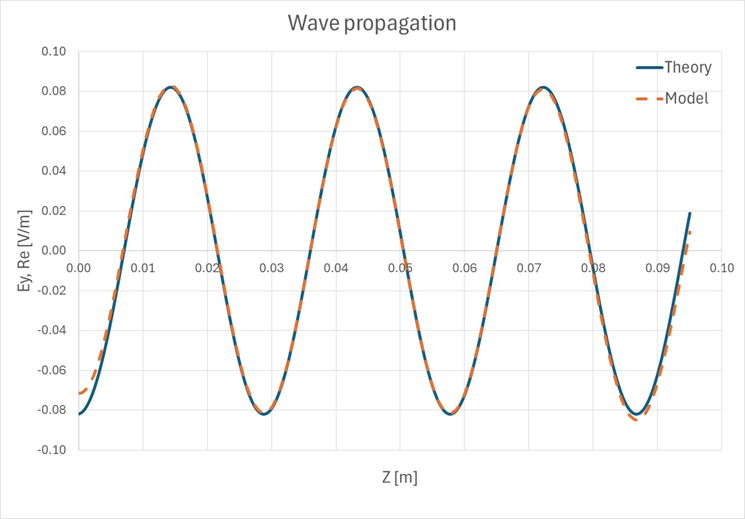




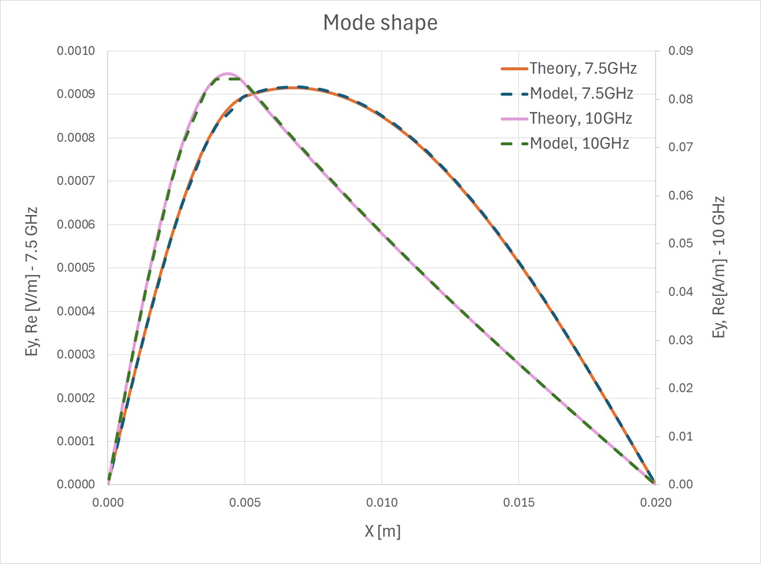
上記の電界分布の式を次のグラフで説明します(ここで、xは波の伝播方向に対して直行であり、サンプリングラインは、電界分布の最大を通っています):Figure 10. さまざまな周波数の基本モードにおける、理論上およびモデル化された電界分布の比較

1 Pozar, D.M., Microwave Engineering, 4th Edition, John Wiley & Sons, Inc., 2012, p.119.